My daughter is in Year 5 and yes it is NAPLAN year; even if I’ve forgotten this fact, her homework would have reminded me. She has just finished worksheets on multiples and factors – including concepts of highest common factor, lowest common multiple. She told me they haven’t been taught in class – which, if it boils down to it, is going to be her word against the teacher’s. And that’s not really what I’m posting about. Nor is this post about worksheets and homework.
This post is about multiplication and using the times table.
As a high school teacher, I know that some kids struggle multiples and factors conceptually. Once applied in fractions and Algebra, the confusion mounts. A good foundation built up through primary/elementary school years cannot be under-rated.
One of the problems I think is that kids really don’t know, i.e. memorised, their times tables. Though they conceptually know of multiplication, or even have several models of it, many still have to calculate often by repeated addition through to college/university as @angrymath tells us (and I can believe it). If you think Cognitive Load Theory makes sense, it follows that knowing one’s times tables reduces the cognitive load when doing maths. There are also strategies – even ‘tricks’ – to help. One of the strategies I teach my kids (my daughters and students alike) is what I call the “goalpost multiplication” approach. Briefly, estimate to the nearest goalpost (x2, x5, x10) and work up or down. For example, 8×7 = 8×5 + 7 + 7. Note that even in this strategy, there is a need for conceptual understanding (and review) of certain concepts such as associative property and number sense via estimation.
That was a dense paragraph and there are things I’d like to qualify:
- I don’t advocate rote learning at the expense of conceptual understanding
- I think Cognitive Load Theory makes sense and I have noted that students who expend much effort (use of working memory) calculating relative to effort on mathematical thinking (e.g., application of calculations) tend to have lower self-concept with regards to their numeracy
- Memorising the times table is not necessary but useful, if just to reduce cognitive load and corollary, improve self-concept with regards to maths
- If you really cannot bear to memorise the times table, at least have some strategies to get you by. As a teacher, help your students learn these strategies
Ok. so here’s what I did with my daughter.
I whipped out the Times Table (here’s one you can grab, too)
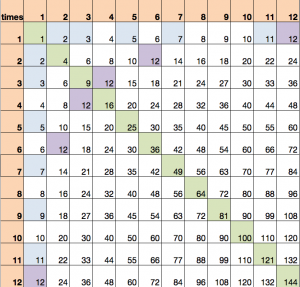
I used this multiplication grid as a visual aid to explain/highlight the following points:
- Any number multiplied by 1 is itself; one day, she’ll learn that this is called multiplicative identity property
- The green line is the square of numbers showing, for example that 3 x 3 = 9 “boxes”
- The green line is like a mirror, a line of symmetry, so one side is the reflection of the other showing 3 x 4 = 4 x 3; one day, she’ll learn that this is called the commutative property of multiplication
- Rows or columns are multiples of that number (in orange)
- The factors of a number are the numbers you multiply to get that number, i.e. the headings in orange
- A number that only shows up in row/column 1 (numbers in blue) means it is a prime number, i.e. its factors are only 1 and itself
- A number repeating across the table left-to-right, say, means it is a common multiple – a multiple shared by the numbers with it as a multiple (e.g. 12 in purple is a common multiple of 1, 2, 3, 4, 6, 12)<most kids this age understand the concept of common – use this to connect to maths; this highlights literacy as well as help build confidence, i.e. common multiple is not such an alien concept after all>
- A number repeating across the table means it has several factors (e.g. 12 in purple shows up in 1, 2, 3, 4, 6, and 12 and these are its list of factors)
- A common factor is a factor that is shared by 2 or more numbers. <this is harder to show using the times table but build on concepts of common and factor list>
One could reasonably argue that teaching all points above is risking cognitive overload. Teaching one-on-one, I could tell that she was keeping pace especially using the times table as visual aid. My first attempt failed just using the definitions on the worksheets; the times table definitely helped.
I also found out that the tables they have at school where the other kind designed for rote learning: 2 x 2 = 4, 2 x 3 = 6, 2 x 4 = 8, etc. She was quite pleased with this multiplication grid and using it for finding patterns (pre-Algebra skills) and not just as direct reference.
To be honest, I don’t mind if she forgets all of the “definitions” above if she can work to find them again. Given the iterative nature of the Maths syllabus, she undoubtedly will have lots of opportunities to re-visit this.
As an aside, creating a multiplication grid using a spreadsheet with formulas and auto-fill would make a good little tech-integration task and exercise of Algebraic skills; there’s more than 1 algorithm.


Great definitions and a wonderful way to teach them. I agree, showing students the concepts, revealing that there is an observable and searchable pattern to them, and matching those concepts to vocabulary is far better than telling them these things. I particularly like definitions 7 and 8. Few people remember to teach these and logic leap into GCF and LCM. This immediately opens the door to confusion and misconception.
For definition 9, I think highlighting the multiples along with the repeating products for two or more products would reveal, by overlap or mix of colour, where common factors are. The greatest of these can then be pointed out and the pattern that the farthest left or down is the GCF revealed.
Definition 10, that of the LCM, would reverse this, where the products of two or more multiples overlap at several values and the least, or rightmost or upmost, of these is the LCM. I think this one would be harder to illustrate than GCF due to the many ways the products are expressed in the multiplication table. For instance, 3x is expressed in a column, in a row and in jumps of three along the multiplication grid. Doing the same with, say, 4x could result in some visual confusion, though cognitive understanding should still be possible.
Ah! There I go revealing that I don’t know my left from my right. 😉
Thanks Shawn…even with the left-and-right confusion. 🙂
We did try to use the grid for LCM and GCF (we use HCF here and highest makes better sense than greatest, imho). It got a little confusing – and would have been even more confusing to explain via a blog post! Working on an analog copy, it was far easier to just list down; she ordered the numbers in her head. I’m fine with this, because as she found out, this grid stopped at 12.
We also had a little chat similar to what you said which directly related multiples and factors but she got a little confused – cognitive overload. 🙂
I am sooooo glad you picked up on my focus on literacy and connecting it with numeracy. I often tell students that terms are meaningful and it is possible to work out what they mean….usually.
cheers.
Maylin- this is a fantastic post. I’ll need to re-read in a couple of days to make sure I have taken it all in.
Multiplicative thinking is so vexed. Over-reliance on drill clearly has failed over the decades. One aspect of your approach which I think is brilliant is the emphasis on terminology connected to a visual graphic.
Thanks
Thanks Peter.
Working with maths strugglers in high school has really made me think about what can be done to ‘prevent’ the struggle in HS, i.e. what foundational stuff can we put in place in primary schools?
A good understanding of multiplication is important. That includes knowing different models, not just the repeated addition.
As mentioned, emphasis on literacy (including, but not limited to, terminology) helps.
I’ve never used the times table grid as a visual aid before. This is practically a eureka moment for me!!! This mash-up of numbers and patterns plus a hint of Geometry (axis of symmetry) is how I like to teach.
cheers.
Thanks for a great post. I also find it very distressing seeing my high school students struggling with this – even to the point of crying (the students). Agree totally with the cognitive load view – knowing your tables reduces the cognitive load freeing up capacity for higher level task and, perhaps even more importantly, removes emotional angst when learning fractions, percentages and algebraic multiplication and division. You can literally see students struggling to work out multiplication facts and sweating/stressing in the process.
I was thinking earlier this week it would be interesting for each student to shade in the table indicating how fluent they are on each multiplication fact. That way we can see the ‘grey areas’ and focus on them. I know I have a grey area in the centre around the 8×7 region – and I’m a maths teacher.
Thinking about my own ‘grey zone’ – I think it comes from my own decision as a child NOT to learn the higher tables since I could ‘easily work them out’. So I have had to live with that extra processing ever since. I suspect many other children who see the patterns in the table make similar decisions not memorise the table – suggesting difficulties with multiplication tables is not necessarily a sign of a general difficulty with mathematics, but an undiagnosed/uncorrected gap in primary school learning. Might be time for all Stage 4 high school teachers to integrate learning multiplication tables into daily practice.
Thanks Nordin.
Interesting theory re: grey area. I have a ‘trick’ for the 6-9 times tables. I don’t teach it to my students nor even my daughters. Interestingly, I feel it needs to be earned – I haven’t really thought deeply why.
Anyway, Stage 1-3 curriculum does not actually require the kids to know all their times table. From memory (which could be wrong), it’s only 2, 5, and 10. So, the grey areas are set. 🙁
I had an interesting chat with a primary teacher looking for ways to teach multiplication about a year ago. Back then I replied that kids understand the concept but they can’t remember the “facts” and then think/believe that they don’t know multiplication. Deliberate practice (some say drill) is the only way I know to do this. I still think this reply holds but if I could go back, I could at least tell him about the above.
The above really made me see why kids struggle with fractions. I heard/read somewhere that there is a correlation between fractions in Algebra in that if you struggle with fractions, you won’t get Algebra.
I have this itch to work in primary. It goes stronger by the day! 🙂
I used to play a game called Multo the kids really enjoyed to learn their tables. They would have a copy of the times table grid by their side. They would then draw up a 4 X 4 grid and fill it with multiples of the times tables. They would start with their 2 and 3 times tables and choose random multiples from their tables like 4 or 9 or 3 or 12….whatever they liked.
Then you would have all of times table question cards like 2 X 2 or 4 X 4 and so on. Just the whole set of the tables they are working on. You put these cards in a container in the middle of a group table of kids competing in multo.
When they have finished writing all their multiples into their 4 X 4 grid they then take turns to pull a card out of the ‘hat’ and if they have the answer to that card they can cross it off their grid.
When they have four in a row – vertically, horizontally or diagonally they then yell bingo!!
After a while they get it that if they choose a number like 24 or 12 or 36 etc with lots of factors they increase their chances of winning at multo. It is part of the Counting On Program. I used to deliver this numeracy program to targetted kids in Year 7 🙂 Other great games too.