My daughter is in Year 5 and yes it is NAPLAN year; even if I’ve forgotten this fact, her homework would have reminded me. She has just finished worksheets on multiples and factors – including concepts of highest common factor, lowest common multiple. She told me they haven’t been taught in class – which, if it boils down to it, is going to be her word against the teacher’s. And that’s not really what I’m posting about. Nor is this post about worksheets and homework.
This post is about multiplication and using the times table.
As a high school teacher, I know that some kids struggle multiples and factors conceptually. Once applied in fractions and Algebra, the confusion mounts. A good foundation built up through primary/elementary school years cannot be under-rated.
One of the problems I think is that kids really don’t know, i.e. memorised, their times tables. Though they conceptually know of multiplication, or even have several models of it, many still have to calculate often by repeated addition through to college/university as @angrymath tells us (and I can believe it). If you think Cognitive Load Theory makes sense, it follows that knowing one’s times tables reduces the cognitive load when doing maths. There are also strategies – even ‘tricks’ – to help. One of the strategies I teach my kids (my daughters and students alike) is what I call the “goalpost multiplication” approach. Briefly, estimate to the nearest goalpost (x2, x5, x10) and work up or down. For example, 8×7 = 8×5 + 7 + 7. Note that even in this strategy, there is a need for conceptual understanding (and review) of certain concepts such as associative property and number sense via estimation.
That was a dense paragraph and there are things I’d like to qualify:
- I don’t advocate rote learning at the expense of conceptual understanding
- I think Cognitive Load Theory makes sense and I have noted that students who expend much effort (use of working memory) calculating relative to effort on mathematical thinking (e.g., application of calculations) tend to have lower self-concept with regards to their numeracy
- Memorising the times table is not necessary but useful, if just to reduce cognitive load and corollary, improve self-concept with regards to maths
- If you really cannot bear to memorise the times table, at least have some strategies to get you by. As a teacher, help your students learn these strategies
Ok. so here’s what I did with my daughter.
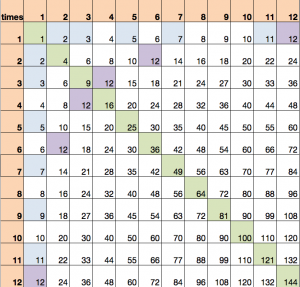
I whipped out the Times Table (here’s one you can grab, too)
I used this multiplication grid as a visual aid to explain/highlight the following points:
- Any number multiplied by 1 is itself; one day, she’ll learn that this is called multiplicative identity property
- The green line is the square of numbers showing, for example that 3 x 3 = 9 “boxes”
- The green line is like a mirror, a line of symmetry, so one side is the reflection of the other showing 3 x 4 = 4 x 3; one day, she’ll learn that this is called the commutative property of multiplication
- Rows or columns are multiples of that number (in orange)
- The factors of a number are the numbers you multiply to get that number, i.e. the headings in orange
- A number that only shows up in row/column 1 (numbers in blue) means it is a prime number, i.e. its factors are only 1 and itself
- A number repeating across the table left-to-right, say, means it is a common multiple – a multiple shared by the numbers with it as a multiple (e.g. 12 in purple is a common multiple of 1, 2, 3, 4, 6, 12)<most kids this age understand the concept of common – use this to connect to maths; this highlights literacy as well as help build confidence, i.e. common multiple is not such an alien concept after all>
- A number repeating across the table means it has several factors (e.g. 12 in purple shows up in 1, 2, 3, 4, 6, and 12 and these are its list of factors)
- A common factor is a factor that is shared by 2 or more numbers. <this is harder to show using the times table but build on concepts of common and factor list>
One could reasonably argue that teaching all points above is risking cognitive overload. Teaching one-on-one, I could tell that she was keeping pace especially using the times table as visual aid. My first attempt failed just using the definitions on the worksheets; the times table definitely helped.
I also found out that the tables they have at school where the other kind designed for rote learning: 2 x 2 = 4, 2 x 3 = 6, 2 x 4 = 8, etc. She was quite pleased with this multiplication grid and using it for finding patterns (pre-Algebra skills) and not just as direct reference.
To be honest, I don’t mind if she forgets all of the “definitions” above if she can work to find them again. Given the iterative nature of the Maths syllabus, she undoubtedly will have lots of opportunities to re-visit this.
As an aside, creating a multiplication grid using a spreadsheet with formulas and auto-fill would make a good little tech-integration task and exercise of Algebraic skills; there’s more than 1 algorithm.