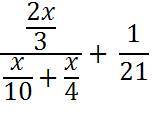Tag: LifeSkills

Problems vs Exercises

Leave a comment

Problems vs. Exercises

Inspired by a blogpost by David Cox (@dcox21), I decided to use the same problem and added an extra fraction. Anyone following me for some time would see that I value mathematical thinking and, as David said, this is a good one to show problem-solving skills. I think it’s also a good one to revise, reinforce and connect mathematical skills (or tools as David calls them).

Simplify:

algebraic fractions

I asked the class what their first thoughts were upon seeing this problem on the board:

  1. “It looks complicated”
  2. “It’s hard”
  3. “It looks like a big problem with lots of little problems”

They were all correct, of course, and I told them so (affirmation is good). I then told them that, in fact, they already have all the skills to solve this problem and they looked at me to as if I’ve gone mad. I suggested that, because it did look complicated, we look at the little problems that make up the big problem to make it easier (note the use of their responses; affirmation is good – oops, said that already).

I then asked what the problem looked like, that is, what’s familiar about the problem.

1. Dividing fractions
2. Adding fractions
3. Algebra – use of pronumerals/letters

Upon revising the above, we added 2 more:

4. Multiplying fractions (division of fractions as multiply by inverse/reciprocal)
5. Order of Operations (fraction bar as a grouping symbol)

And so we set off to solve the problem and they asked for more to practice on, an Exercise as David puts it. This was the desired and expected effect. I used a similar approach when I introduced Decimals to my year 7 class last year (note to self: must share/blog this resource).

I should have also pointed out that this sort of thinking/questioning/problem-solving approach can be applied in real life. Sometimes problems we face in life can seem hard and complex yet often, with chunking (or breaking down into smaller bits), we find that we have the skills/tools to solve them.

Parents as partners in teaching

Leave a comment

If education serves the purpose of preparing children to be responsible adults then I believe parents have a significant role. Such an education can not practically be the sole responsibility of schools.

Many parents I know, myself included, are interested in what their children are doing and learning. There can be issues that range from language, time constraints and ability levels to just sheer inability of some children to articulate what is going on in a way that parents can connect with. This article from the UK Guardian, Parents struggle to help with homework, have some salient points.

Even anecdotally, I know that Maths is a subject most parents are reluctant to help with. Prior to becoming a maths teacher, I can list a few reasons why: (1) changes in terminology, (2) changes in methods, and (3) what teachers say take precedence over what parents say. There may be a seed of truth in the Guardian article mentioning that parents can do more harm than good. I remember a time when a Year 7 parent asked why her daughter has not been taught the “multiplicative inverse in the division of fractions”. Seriously, in year 7!  For the record, it was taught but without the snazzy words. Apropos, the term we now use – reciprocal – is not necessarily more meaningful.

One of the things I’ve done to empower parents is to create a class website on Weebly. If nothing else, I hope to tell parents a little bit about the terms and methods discussed in class, e.g. I never used pronumerals when learning Algebra, ditto many parents, for sure. How I was taught maths is not how I’m teaching it  (see previous post).

I don’t aim it to be a maths website replicating a myriad of resources but rather a portal into my class with pre-selected resources actually used in class and accessible from home. This does not replace the website we have in the school portal which contains far more detail, especially at the operational lesson-level. This also does not replace the usual channels of communication: phone, email and Parent/Teacher interviews.

Serendipitous to the day I read the Guardian article, I’ve had some discussions with more experienced teachers about the website’s sustainability and value. I have no qualms saying that it is sustainable enough given my vision for it; also, I find Weebly easy enough to use (I recommend it) . I am less sure about the site’s value. What can I say? It is like leading a horse to the water with no guarantee that it will drink. I did have one parent email me to say that he appreciates having it.  That is enough, for now. That and the fact that, as a parent, I see its value as well. A bit of context: parents have limited access to the school portal hence the push for an external web.

Parents can be partners in teaching. Mostly, they want to be. As teachers, here is an untapped resource that, with a bit of help and communication, can help achieve better outcomes for our students. By the way, I am all for parents – and teachers – modelling how to handle being stumped and making mistakes. Perhaps naively, I don’t agree that parents helping can do more harm than good.

Spreadsheets, Budgets and Formals

Leave a comment

I’m not a big fan of spreadsheets – prefer databases more – but it needs to be taught. It can be a useful tool in life. Engaging and motivating low-ability year 10 maths students can be challenging the best of times. Here is a lesson I prepared that would teach them a life skill of budgeting using spreadsheets.

Lesson Activity

Year 10 formals is months away but this is something most year 10 girls are excited about. So when I said we’ll create a budget for it, everyone was excited to talk about something interesting.  Motivation covered!

  1. Brainstorm budget items (“What do I need for the formals?”) – emphasise no right or wrong answer, if not personally relevant then just set the budget to $0. The point of this step is to engage.
  2. Create a new spreadsheet and enter all the items under the heading of “What I need”. Good opportunity to revise basics of file creation/saving, renaming worksheet (Budget), data entry and Format-ting text and columns
  3. Add new columns with headings of Min, Max, Range (excellent chance to revise these statistical concepts). Each student enters their own budget, again no right or wrong. Format columns to currency.
  4. Calculate Range (=Max -Min columns); revise/teach use of Excel functions and autoFill.
  5. Calculate minimum and maximum budget totals; use autoSum or use SUM function
  6. With 9 months to go, create a monthly savings budget (=total / 9); some students don’t know the division symbol in Excel
  7. What are your cheapest (use MIN function) and most expensive (use MAX function) items
  8. Email your spreadsheet (make sure they all know how to attach files to email)

Discussion points

  • Can you afford your monthly budget (minimum, maximum)?
  • What adjustments can you make to afford the items? Are you working?
  • Would you consider borrowing or even doing without?
  • Would you negotiate with your parents? Can your budget spreadsheet help you talk to them?

Reflection

The girls enjoyed this lesson. The discussions were interesting and for my part, enlightening: truly amazing what teenagers deem they need and how different they all can be. They did not even mind the spreadsheet and statistics bit and were all keen to follow the flow of the lesson. They compared their results and even they were amazed at how different they all were.

I like this lesson because it was relevant, engaging and differentiated.